VB .NET - Números e seqüência de Fibonacci

 Neste artigo eu vou mostrar como calcular a sequência de Fibonacci usando a linguagem VB .NET.

Tudo começou com  Leonardo de Pisa (Fibonacci=filius Bonacci=filho de Bonacci) matemático e comerciante da idade média, que em 1202 publicou um livro - Liber Abbaci -  onde descreveu o crescimento de uma população de coelhos , que viria trazer o conhecimento ao mundo ocidental dos números e seqüência que ficou conhecida como números de Fibonacci.

Mas quais seriam esses números e como obtê-los ?

Olhe com atenção a seqüência de números abaixo:

F = 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,144, 233, ...

Repare que, exceto para os dois primeiros termos (1 e 1 ), todos os outros podem ser calculados iterativamente a partir da soma dos dois termos imediatamente anteriores.   

Assim o algoritmo para obter um número de Fibonacci pode ser expresso da seguinte forma:

M(1) = 1;
M(2) = 1;
M(n) = M(n-1) + M(n-2), para n > 2

Curiosidades sobre a seqüência de Fibonacci
                                                                                 ___  
O número de ouro tem o valor obtido por phi =  ( 1 + \/  5     ) / 2

que é igual a 1,618 033 989...

Mas o que isso tem a ver com os números de Fibonacci ?

Como se lembram a Seqüência de Fibonacci possui a seguinte sequência de números 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233....

 

Se dividirmos cada um dos números pelo seu antecedente, reparamos que essa razão vai tender para um certo valor.

 

Ou seja, se fizermos F2/F1=1; F3/F2=2; F4/F3=1,5; F5/F4=1,6(6); F6/F5=1,6 e se continuarmos assim sucessivamente, obtemos a seguinte sequência de números:

 

1,000 000; 2,000 000; 1,500 000; 1,666 666; 1,600 000; 1.625 000; 1,615 385; 1,619 048; 1,617 647; 1,618 182; 1,617 978; 1,618 056; 1,618 026; 1,618 037; ... 
Uma seqüência de números irracionais.

 

Então Fn+1/Fn aproxima-se cada vez mais de Phi.


Vejamos outras curiosidades sobre os números de Fibonacci: (http://www.infoescola.com/matematica/sequencia-de-fibonacci/)

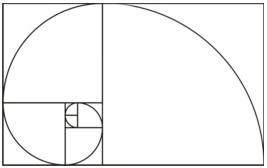
A partir de dois quadrados de lado 1, podemos obter um retângulo de lados 2 e 1. Adicionando a esse retângulo um quadrado de lado 2, obtemos um novo retângulo 3×2.Adicionando agora um quadrado de lado 3, obtemos um retângulo 5×3. Na figura a seguir e veja que os lados dos quadrados que adicionamos para determinar os retângulos formam a seqüência de Fibonacci.

Se utilizarmos um compasso e traçarmos o quarto de circunferência inscrito em cada quadrado, encontraremos uma espiral formada pela concordância de arcos cujos raios são os elemento da seqüência de Fibonacci.

O Partenon foi construído em Atenas pelo arquiteto grego Fidias. A fachada principal do edifício, hoje em ruínas, era um retângulo que continha um quadrado de lado igual à altura. Essa forma sempre foi considerada satisfatória do ponto de vista estético por suas proporções sendo chamada retângulo áureo ou retângulo de ouro.

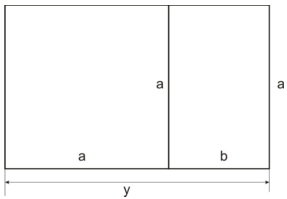
Como os dois retângulos indicados na figura são semelhantes temos:

Como:

Substituindo (2) em (1) temos:

Resolvendo a equação:

Chegamos a :

Esse número é conhecido como número de ouro (phi) e pode ser representado por:

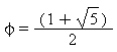
A soma de uma seqüência de Fibonacci

Para saber a soma de uma seqüência de Fibonacci basta pular dois termos à frente do último número e subtrair o valor 1.

Qual a soma da seguinte seqüência de Fibonacci : 1, 1, 2, 3, 5, 8, 13, 21, 34

Elementar: 

1- salte dois números a frente do último número: 34 -> 55 -> 89
2- Subtrai 1 :  89 -1 = 88
3- A soma é igual a 88   (1+ 1+ 2+ 3+ 5+ 8+ 13+ 21+ 34 = 88)

Esta pequena introdução é apenas para aguçar a sua curiosidade para a pesquisa. neste fascinante mundo da matemática.

O que nos interessa mesmo é mostrar como podemos implementar a geração da seqüência de Fibonacci e como obter um elemento da seqüência usando a linguagem VB .NET.

Existem muita formas de implementar a geração dos números de Fibonacci e obter um elemento da seqüência usando o VB .NET e eu vou mostrar duas implementação simples.

Os algoritmos que eu vou usar neste artigo foram encontrados na web e eu só fiz um ajuste: Eu entendo que a seqüência de Fibonacci começa com o número 1 e não com o número zero como indica a Wikipédia e outros sites, portanto com base neste meu entendimento fiz as alterações quando necessário.

Vamos criar uma aplicação Windows Forms  usando o Visual Basic 2010 Express Edition para obter a série de Fibonacci e também para obter um determinando elemento da série.

No menu File -> New Project , selecione a seguir Windows Forms Application e a linguagem Visual Basic informando o nome Fibonacci;

O leiaute da aplicação pode ser visto na figura abaixo e é bem simples . Usamos dois controles ListBox, dois controles TextBox e 3 controles Buttons;

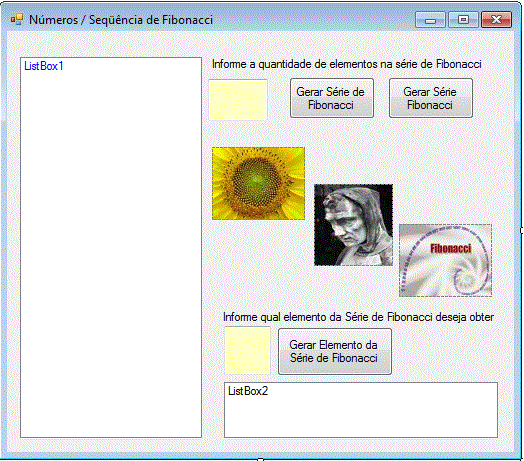Primeiro vamos mostrar dois algoritmos para obter uma seqüência de Fibonacci : um usando recursão e outro sem usar recursão.

Vamos incluir uma classe no projeto chamada Fibonacci no arquivo Fibonacci.vb e na classe definir estes dois algoritmos para retornar um seqüência de Fibonacci sem usar recursão conforme o código abaixo:

1- Código para gerar uma seqüência de Fibonacci sem usando recursão e retornado um Array:

 Public Shared Function fibonacciComRecursaoArray(ByVal  tamanho As Integer) As Array

        Dim i As Double = 2
        Dim fibonacci(tamanho - 1) As Double
        fibonacci(0) = 1
        fibonacci(1) = 1

        While i <> tamanho
            fibonacci(i) = fibonacci(i - 1) + fibonacci(i - 2)
            i += 1
        End While

        Return fibonacci

    End Function

O parâmetro tamanho refere-se a quantos elementos na seqüência desejamos gerar.

2-  Segundo Código para gerar uma seqüência de Fibonacci sem usar a recursão e retornado um Array:

 Public Shared Function CalculaFibonacciSemRecursao(ByVal limite As Double) As Double()

        Dim resultado(limite - 1) As Double
        Dim antUm, antDois, total As Double

        antUm = 1
        antDois = 1

        For i = 0 To limite - 1
            If i = 0 Then
                total = 1
                resultado(i) = total
            ElseIf i = 1 Then
                total = 1
                resultado(i) = total
            ElseIf i >= 2 Then
                total = antUm + antDois
                antDois = antUm
                antUm = total
                resultado(i) = total
            End If
        Next

        Return resultado
    End Function

 

Obs : Você pode usar o novo namespce System.Numerics que contém a classe BigNumber e fornece métodos estáticos para diferentes operações matemáticas.

Abaixo um versão usando o BigInteger: (Somente disponível na versão 4.0 da plataforma .NET)

 Public Function Fibonacci(ByVal limite As Integer) As BigInteger

        Dim valorAnterior = New BigInteger(-1)
        Dim valorAtual = New BigInteger(1)

        For i = 0 To limite
            Dim soma = valorAtual + valorAnterior
            valorAnterior = valorAtual
            valorAtual = soma
        Next

        Return valorAtual
    End Function

A seguir vamos definir dois métodos para obter um elemento da seqüência gerada:

1 - Código para obter um elemento de Fibonacci sem usar recursão:

 Public Shared Function GetNumeroSequenciaFibonacci(ByVal fibIndex As Double) As Double

        If (fibIndex < 2) Then
            Return fibIndex
        End If

        Dim FibArray(2) As Double
        Dim i As Double

        FibArray(0) = 0
        FibArray(1) = 1

        For i = 2 To fibIndex
            FibArray(1) = FibArray(1) + FibArray(0)
            FibArray(0) = FibArray(1) - FibArray(0)
        Next

        Return FibArray(1)

    End Function

1 - Código para obter um elemento de Fibonacci  usando recursão:

Public Shared Function fibonacciRetornaElemento(ByVal i As Integer) As Integer

        If i < 2 Then
            Return i
        Else
            Return fibonacciRetornaElemento(i - 1) + fibonacciRetornaElemento(i - 2)
            Application.DoEvents()
        End If

    End Function

Com isso já temos a classe com os métodos prontos para serem usados. Observe que eu defini os métodos como shared de forma que não precisaremos criar uma instância da classe para usá-los.

No formulário do projeto iremos usar o evento Click dos botões de comando para chamar o método respectivo.

Vamos definir no início do formulário as variáveis abaixo para podermos calcular o tempo gasto em cada operação:

Shared inicio As DateTime
Shared fim As DateTime
Dim tempo_gasto As TimeSpan

No evento click do botão - Gerar Série de Fibonacci I - vamos incluir o seguinte código:

 Private Sub btnSerieFibonacci_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles btnSerieFibonacci.Click


        Dim i As Double

        Dim cont As Double = 1

        i = CInt(txtValor.Text)

        inicio = Now

 

        Dim vet As Array = Fibonacci.CalculaSequenciaFibonacci(i)

 

        ListBox1.Items.Clear()

        For Each i In vet

            ListBox1.Items.Add(cont & "- " & i)

            cont = cont + 1

        Next

 

        fim = Now

        tempo_gasto = fim.Subtract(inicio)

        lbltg1.Text = tempo_gasto.TotalSeconds.ToString("0.000000")

 

    End Sub

No evento click do botão - Gerar Série de Fibonacci II - vamos incluir o seguinte código:

Private Sub btnGerarSerieFibonacciSemRecursao_Click_1(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles btnGerarSerieFibonacciSemRecursao.Click

        Dim i As Double

        Dim cont As Double = 1

        i = CInt(txtValor.Text)

        inicio = Now

 

        Dim vet As Array = Fibonacci.fibonacciSequenciaArray(i)

 

        ListBox1.Items.Clear()

        For Each i In vet

            ListBox1.Items.Add(cont & "- " & i)

            cont = cont + 1

        Next

 

        fim = Now

        tempo_gasto = fim.Subtract(inicio)

        lbltg2.Text = tempo_gasto.TotalSeconds.ToString("0.000000")

 

    End Sub

Executando o projeto iremos obter:

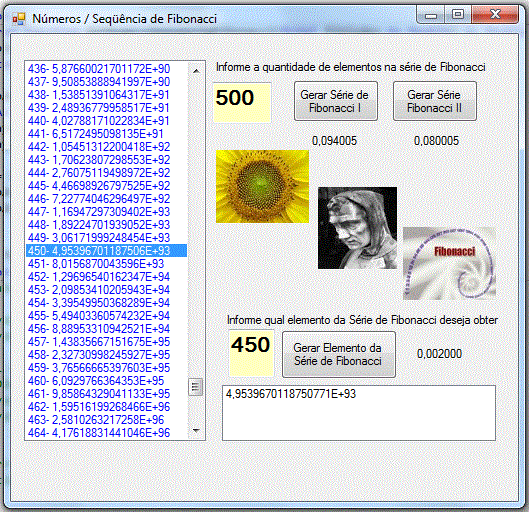Pegue o projeto completo aqui:  Fibonacci.zip

Aguarde mais artigos sobre VB .NET

Referências:

 

José Carlos Macoratti