![]() .NET
- Números Perfeitos ( VB .NET, C# e VB6)
.NET
- Números Perfeitos ( VB .NET, C# e VB6)
O que é um número perfeito ?
Em Matemática, um número perfeito é um número inteiro para o qual a soma de todos os seus divisores positivos próprios (excluindo ele mesmo) é igual ao próprio número.
Por exemplo 6 é um número perfeito, pois 1 + 2 + 3 = 6
O número 28 também é um número perfeito pois temos que seus divisores : 1 + 2 + 4 + 7 + 14 = 28
O número 496 é outro número perfeito visto que: 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496
Euclides descobriu que os quatro primeiros números perfeitos são gerados pela fórmula: 2n-1(2n - 1):
O quinto número perfeito é o número 33.550.336 => 212(213 - 1)
E o sexto número perfeito é : 8.589.869.056. Ufa...
Mas o que tem a ver número perfeito com linguagem de programação VB .NET ou C# ?
É porque eu quero aproveitar o assunto para introduzir o conceito de algoritmo.
Mas o que é um algoritmo ?
Um algoritmo nada mais é do que uma receita que mostra passo a passo os procedimentos necessários para a resolução de uma tarefa.
Pense em uma receita de bolo que primeiro define os ingredientes e depois o modo de preparar o bolo. Podemos considerar uma receita de bolo como um exemplo de um algoritmo bem simples.
Em termos mais técnicos podemos dizer que um algoritmo é uma sequência lógica, finita e definida de instruções que devem ser seguidas para resolver um problema ou executar uma tarefa.
Um algoritmo pode ser muito simples ou bem complexo envolvendo repetições de passos (iterações), toma de decisões com comparações ou lógica para que a tarefa seja concluída.
Um programa de computador é essencialmente um algoritmo que diz ao computador os passos específicos e em qual ordem eles devem ser executados, como por exemplo, os passos a serem tomados para calcular as notas que serão impressas nos boletins dos alunos de uma escola.
Logo, o algoritmo pode ser considerado uma sequência de operações que podem ser depois implementadas em qualquer linguagem de computador. Um algoritmo é assim independente de qualquer linguagem de programação.
Exemplo de um algoritmo bem simples:
Algoritmo de domingo.
Acordar.
Escovar os dentes.
Tomar o café.
Se estiver sol vou passear senão leio o jornal.
Almoçar.
Ir ao cinema.
Fazer uma refeição.
Ir dormir.
Final do domingo.
|
Vamos partir do conceito de número perfeito para propor o seguinte problema :
Elabore um algoritmo para determinar se um dado número n é um número perfeito.
Para resolver um problema no computador é preciso que seja primeiramente encontrada uma maneira de descrever este problema de uma forma clara e precisa.
É preciso encontrar uma seqüência de passos que permita resolver o problema de maneira automática e repetitiva.
Além disto é preciso definir como os dados processados serão armazenados no computador.
Portanto, a solução de um problema por computador é baseada em dois pontos:
Isso nada mais é que um Algoritmo.
Vejamos alguns exemplos de algoritmos propostos para resolver o problema:
| algoritmo "numero_perfeito" var i,n,soma: inteiro inicio leia (n) soma <- 0 para i de 1 ate n-1 faca se n % i = 0 entao soma <- soma + i fimse fimpara se soma=n entao escreva ("Numero Perfeito") senao escreva ("Nao e um numero perfeito") fimse fimalgoritmo |
inicio inteiro: i, j, numero, somaDivisores ; para i <- 1 ate 10 faca leia (numero) ; somaDivisores <- 0 ; para j <- 1 ate numero faca se (numero mod j = 0) entao somaDivisores <- somaDivisores + j ; fimse fimpara se (somaDivisores = numero) entao imprimir("PERFEITO") senao imprimir("NÃO É PERFEITO") fimse fimpara fim |
algoritmo "NumeroPerfeito" // Seção de Declarações var n, perf, cont: inteiro inicio escreva("Informe um numero") leia(n) para cont de 1 ate n - 1 faca se (n mod cont = 0 ) entao perf <- perf + cont fimse fimpara se (perf = n) entao escreval (n, " é perfeito ") senao se (perf <> n) entao escreval(n, "Nao é perfeito") fimse fimse fimalgoritmo |
Podemos notar que não usamos uma linguagem de programação em nenhum dos algoritmos propostos visto que o algoritmo tem que ser representado de forma que qualquer pessoa possa entendê-lo.
No nosso exemplo usamos uma linguagem chamada Pseudo-linguagem que é uma linguagem intermediária entre a linguagem natural e uma linguagem de programação de computadores.
Podemos representar um algoritmo usando formas geométricas através de um fluxograma.
Um fluxograma é um diagrama que tem como finalidade representar processos ou fluxos de materiais e operações (diagramação lógica, ou de fluxo)
O fluxograma sempre possui um início, um sentido de leitura, ou fluxo, e um fim.
Obs: Não confunda fluxograma com organograma que representa a estrutura hierárquica e funcional de uma organização.
Abaixo temos as principais formas geométricas usadas nos fluxogramas:
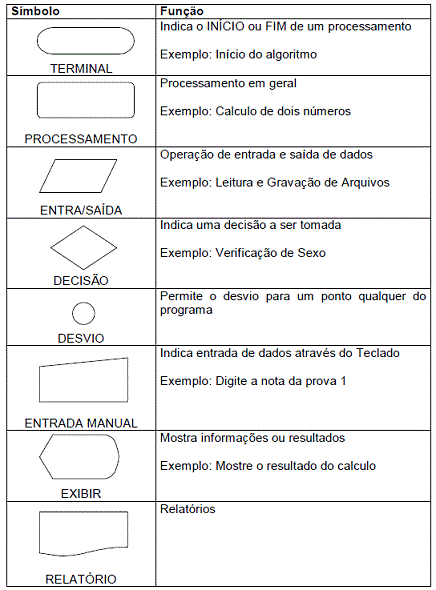 |
Geralmente, usa-se um círculo alongado para indicar o início e o fim do fluxo; - A seta é usada para indicar o sentido do fluxo; - No retângulo são inseridas as ações(processamento); - O losango representa questões/alternativas; - O losango sempre terá duas saídas; - As linhas ou setas nunca devem cruzar umas sobre as outras; - O texto deve ser sempre claro e sucinto; - Recomenda-se iniciar as ações sempre com um verbo no infinitivo (fazer, dizer…); |
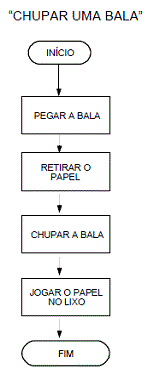
A seguir vemos um diagrama de blocos que representa os passos lógicos de um processo chamado "Chupar Bala":
 |
Abaixo temos um exemplo de um fluxograma representando um algoritmo para somar dois números reais:
 |
| fonte: http://www.prof2000.pt/users/famaral/ig/tlp/fluxogramas.htm (acessado em dezembro de 2012) |
implementando o algoritmo para encontrar números perfeitos em VB .NET , C# e Visual Basic 6
Após definir o algoritmo vou mostrar como implementá-lo usando as linguagens VB .NET , C# e Visual Basic 6.
Eu vou usar as seguintes ferramentas:
1- implementação VB .NET
Crie um novo projeto no do tipo Visual Basic 2010 Express Edition Console Application com o nome VBNET_NumerosPerfeitos:
A seguir defina o código abaixo no modulo Module1:
Module Module1
Dim maximo As Integer = 0
Dim numeroMinimo As Integer = 1 'MINIMO
Dim calulaTotal As Integer = 0
Dim numero As Integer = 0
Dim numeroTratado As Integer = 0
Dim modulo As Integer = 0
Dim numeroDivisor As Integer = 0
Dim valorMaximoInformado As String
Dim valorMaximo As Integer
Sub Main()
Console.WriteLine("+++++++++++++++++++++++++++++++++++++")
Console.WriteLine(" PROCURANDO NÚMEROS PERFEITOS")
Console.WriteLine(" ")
Console.WriteLine("+++++++++++++++++++++++++++++++++++++")
Console.WriteLine(" ")
Console.WriteLine(" ")
Console.WriteLine(" Este programa vai encontrar números perfeitos entre 1 e o número informado")
Console.WriteLine(" Informe o valor máximo : ")
valorMaximoInformado = Console.ReadLine()
Console.WriteLine(" ")
valorMaximo = Convert.ToInt32(valorMaximoInformado)
maximo = valorMaximo
While numeroMinimo <= maximo
If numeroMinimo = 1 Then
numeroTratado = numeroMinimo
numeroDivisor = numero - 1
If numeroDivisor <> 0 Then
modulo = numeroTratado Mod numeroDivisor
End If
If modulo = 0 Then
'acumula totais
calulaTotal += numeroDivisor
End If
Else
For numero = numeroMinimo To 1 Step -1
numeroTratado = numeroMinimo
numeroDivisor = numero - 1
If numeroDivisor <> 0 Then
modulo = numeroTratado Mod numeroDivisor
End If
If modulo = 0 Then
'acumula total
calulaTotal += numeroDivisor
End If
Next
If calulaTotal = numeroTratado Then
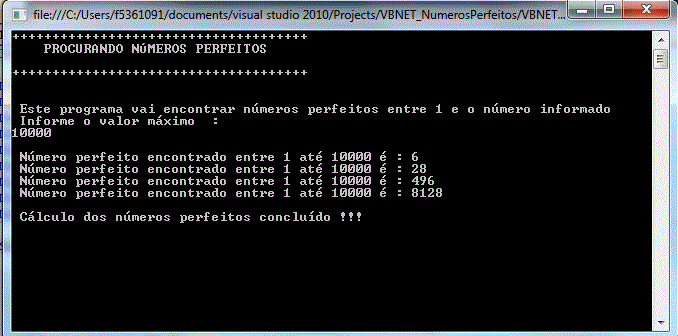
Console.WriteLine(" Número perfeito encontrado entre 1 até {0} é : {1} ", maximo, numeroTratado)
End If
numeroTratado = 0
numeroDivisor = 0
calulaTotal = 0
End If
numeroMinimo += 1
End While
Console.WriteLine(" ")
Console.WriteLine(" Cálculo dos números perfeitos concluído !!!")
Console.ReadLine() 'pausa
End Sub
End Module
|
 |
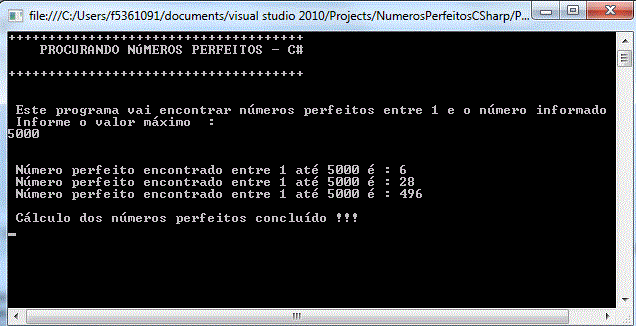
2- implementação C#
Crie um novo projeto no do tipo Visual C# 2010 Express Edition Console Application com o nome CSharp_NumerosPerfeitos:
using System;
public class PerfectNumbers
{
public static void Main()
{
int maximo = 0;
int numeroMinimo = 1;
//MINIMO
int calulaTotal = 0;
int numero = 0;
int numeroTratado = 0;
int modulo = 0;
int numeroDivisor = 0;
string valorMaximoInformado = null;
int valorMaximo = 0;
Console.WriteLine("+++++++++++++++++++++++++++++++++++++");
Console.WriteLine(" PROCURANDO NÚMEROS PERFEITOS - C# ");
Console.WriteLine(" ");
Console.WriteLine("+++++++++++++++++++++++++++++++++++++");
Console.WriteLine(" ");
Console.WriteLine(" ");
Console.WriteLine(" Este programa vai encontrar números perfeitos entre 1 e o número informado");
Console.WriteLine(" Informe o valor máximo : ");
valorMaximoInformado = Console.ReadLine();
Console.WriteLine(" ");
valorMaximo = Convert.ToInt32(valorMaximoInformado);
maximo = valorMaximo;
Console.WriteLine(" ");
valorMaximo = Convert.ToInt32(valorMaximoInformado);
maximo = valorMaximo;
while (numeroMinimo <= maximo) {
if (numeroMinimo == 1) {
numeroTratado = numeroMinimo;
numeroDivisor = numero - 1;
if (numeroDivisor != 0) {
modulo = numeroTratado % numeroDivisor;
}
if (modulo == 0) {
//acumula totais
calulaTotal += numeroDivisor;
}
} else {
for (numero = numeroMinimo; numero >= 1; numero += -1) {
numeroTratado = numeroMinimo;
numeroDivisor = numero - 1;
if (numeroDivisor != 0) {
modulo = numeroTratado % numeroDivisor;
}
if (modulo == 0) {
//acumula total
calulaTotal += numeroDivisor;
}
}
if (calulaTotal == numeroTratado) {
Console.WriteLine(" Número perfeito encontrado entre 1 até {0} é : {1} ",
maximo, numeroTratado);
}
numeroTratado = 0;
numeroDivisor = 0;
calulaTotal = 0;
}
numeroMinimo += 1;
}
Console.WriteLine(" ");
Console.WriteLine(" Cálculo dos números perfeitos concluído !!!");
Console.ReadLine();
//pausa
}
}
|
 |
3 - implementação no Visual Basic 6
Private Sub Form_Load()
s:
Dim k As Integer
Dim per As Boolean
Dim n As Integer
per = False
n = 1
k = InputBox("Informe um número : ", "Número") 'informa um numero
For i = 2 To k ' checa o algoritmo
For r = 2 To k
o = i * r
If o = k Then
n = n + i
End If
Next r
Next i
If n = k Then ' se o número é iguala soma dos divisoers entã conclui
per = True
End If
If per = True Then
MsgBox "Número Perfeito", , "Este número é um número Perfeito"
Else
MsgBox "Não Perfeito", , "Este Número é Não Perfeito"
End If
d = MsgBox("Deseja Continuar ", vbYesNo, "Continuar")
If d = vbYes Then
GoTo s
Else
End
End If
End Sub
|
|
Pegue os projetos completos aqui:
João 10:7
Tornou, pois, Jesus a dizer-lhes: Em verdade, em verdade vos digo: eu sou a porta das ovelhas.João 10:8
Todos quantos vieram antes de mim são ladrões e salteadores; mas as ovelhas não os ouviram.Referências: