![]() VB
.NET - Calculando Permutações
VB
.NET - Calculando Permutações
Hoje vamos falar sobre Permutações.
Se você não fugiu da escola, deve lembrar das aulas de matemática quando algum dia alguém tentou lhe ensinar a calcular permutações.
Vamos então começar lembrando a teoria iniciando com o conceito sobre arranjos...
Arranjos
Arranjos são agrupamentos nos quais a ordem dos elementos faz diferença.
Por exemplo, os números de três algarismos formados pelos elementos {1,2 e 3} são:
312, 321, 132, 123, 213, 231
Esse agrupamento é um arranjo, pois a ordem dos elementos 1, 2 e 3 é diferente; È considerado arranjo simples, pois os elementos não se repetem.
Para que tenhamos arranjos simples é preciso ter um conjunto de elementos distintos com uma quantidade qualquer de elementos, sendo que os arranjos simples formados irão possuir n elementos, e essa quantidade será igual ou menor que a quantidade de elementos do conjunto.
Permutação
O conceito de permutação expressa a idéia de que objetos distintos podem ser arranjados em inúmeras ordens distintas.
Assim, seja um conjunto A com n elementos; chamamos de permutação a todo arranjo com n elementos retirados de A.
A cada um dos agrupamentos que podemos formar com certo número de elementos distintos, tal que a diferença entre um agrupamento e outro se dê apenas pela mudança de posição entre seus elementos, damos o nome de permutação simples.
Exemplos:
1) Seja A um conjunto com os elementos {a, b, c}.
As permutações possíveis de A são: {(a,b,c);(a,c,b);(b,a,c);(b,c,a);(c,a,b);(c,b,a)}. Total de 6 permutações.
2) Quantos anagramas possui a palavra OBA ?
As permutações da palavra são: {(OBA;(OAB);(BAO);(BOA);(ABO);(AOB)}. Total de 6 permutações.
Assim para obter o número de permutações com m elementos distintos de um conjunto, basta escolher os m elementos em uma determinada ordem.
O número de permutações de m elementos será expresso por : P(m)
A expressão para seu cálculo será dada por: P(m) = m(m-1)(m-2)...(m-p+1)...3.2.1
Podemos também escrever : A(m,m) = P(m)
O Arranjo de m elementos dos quais m elementos participam é igual a Permutação destes elementos.
Uma forma simplificada de expressar a permutação de m elementos é através do fatorial: P(m) = m!
Este símbolo de exclamação posto junto ao número m é lido como o fatorial de m, onde m é um número natural.
O fatorial de um número inteiro não negativo pode ser definido de uma forma recursiva através da função P=P(m) ou com o uso do sinal de exclamação:
(m+1)! = (m+1).m! Ex: 3! = 3.2.1! => que é a mesma coisa que : 3.2.1 = 6
Nota : Lembrando que : 0! = 1 (o fatorial de zero é igual a 1) e que 1! = 1 ( o fatorial de 1 é igual a 1)
Com isso creio que já deu para recordar o básico sobre arranjo e permutação simples.
Vamos então ao que realmente interessa...
Como podemos fazer para implementar o cálculo de permutações simples no Visual Basic ?
Calculando permutações com o Visual Basic
Vou mostrar duas possibilidades de calcular permutações usando a linguagem Visual Basic através do Visual Basic 2010 Express Edition.
1- Calculando as permutações de um valor numérico
Na primeira eu vou mostrar como podemos calcular quantas permutações podemos realizar com um determinado valor numérico.
Neste caso irei informar um valor numérico e irei obter a quantidade de permutações possíveis sendo que as possíveis permutações serão exibidas em um controle ListBox.
A interface do programa é bem simples e possui apenas uma caixa duas caixas de texto, um Button e um ListBox.
Abaixo vemos o programa em execução exibindo o resultado para a permutação de 4 elementos:
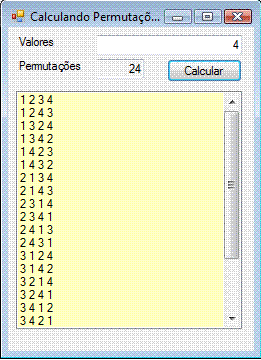 |
| fig 1.0 |
Abra o VB 2010 Express Edition e crie um novo projeto do tipo Windows Forms Application com o nome Permutacoes;
A seguir no formulário padrão inclua os seguintes controles: 2 Labels, 2 TextBox, 1 Button e 1 ListBox conforme o leiaute acima (fig 1.0):
A seguir inclua o código abaixo no formulário form1.vb:
Public Class Form1
Private NumeroValores As Integer
Private m_Usado() As Integer
Private m_SolucaoAtual() As Integer
Private Sub btnCalcular_Click(ByVal sender As System.Object, ByVal e
As System.EventArgs) Handles btnCalcular.Click
lstResultados.Items.Clear()
Application.DoEvents()
'define quantos valores serão permutados
NumeroValores = Val(txtNumeroItens.Text)
ReDim m_Usado(NumeroValores)
ReDim m_SolucaoAtual(NumeroValores)
EnumeraValores(1)
txtCombinations.Text = Format$(Factorial(NumeroValores))
End Sub
Private Sub EnumeraValores(ByVal index As Integer)
' Verifica se existe qualquer valores
If index > NumeroValores Then
' Todos os valores são usados
' Obtem uma string para a solução
Dim resultado As String = ""
For i As Integer = 1 To NumeroValores
resultado &= Format$(m_SolucaoAtual(i)) & " "
Next i
' Inclui a solução a lista
lstResultados.Items.Add(resultado)
Exit Sub
End If
' Examina cada valor
For i As Integer = 1 To NumeroValores
' Verifica se o valor ja foi usado
If Not m_Usado(i) Then
' Se nao foi usado tente usá-lo
m_Usado(i) = True
m_SolucaoAtual(index) = i
EnumeraValores(index + 1)
m_Usado(i) = False
End If
Next i
End Sub
Private Function Factorial(ByVal num As Long) As Long
Dim resultado As Long = 1
For i As Integer = 2 To num
resultado *= i
Next i
Return resultado
End Function
End Class
|
Neste código temos duas funções que são chamadas a partir do evento Click do botão Calcular :
2- Calculando as permutações
Nesta solução vamos calcular a permutação simples possíveis para os itens informados.
O usuário deverá informar os itens separados por vírgulas em uma caixa de texto no formulário da aplicação e as permutações serão calculadas e exibidas.
A interface do programa é similar a usada no programa anterior e nas figuras abaixo vemos o programa em execução mostrando o resultado as permutações para a palavra CASA (anagrama) e para os números 20,11,15,13,80:
 |
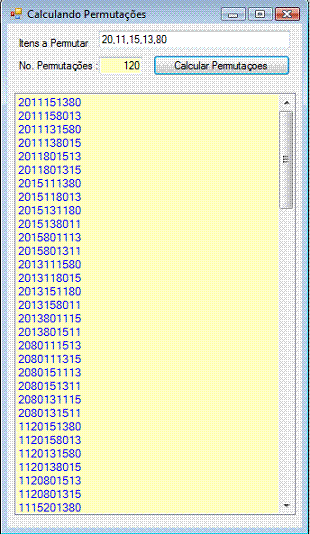 |
Abra o VB 2010 Express Edition e crie um novo projeto do tipo Windows Forms Application com o nome Permutacoes2;
A seguir no formulário padrão inclua os seguintes controles: 2 Labels, 2 TextBox, 1 Button e 1 ListBox conforme o leiaute acima:
A seguir inclua o código abaixo no formulário form1.vb:
Public Class Form1
'Gera e exibe permutações
Private Sub btnCalcular_Click(ByVal sender As System.Object, ByVal e As System.EventArgs)
Handles btnCalcular.Click
lstResultados.Items.Clear()
txtPermutacoes.Text = ""
Application.DoEvents()
Dim matriz() As String
matriz = txtValores.Text.Split(",")
'Genera uma coleção para permutar
'define o total de elementos a permutar
Dim num_valores As Integer = Val(matriz.Length)
Dim valores As New Collection
'Atribui os valores informados aos valores
For i As Integer = 0 To num_valores - 1
valores.Add(matriz(i))
Next i
' Gera as permutações para o no de elementos informados
Dim permutacoes As Collection = GeraPermutacoes(valores)
' Exibe o resultado
For Each p As Collection In permutacoes
Dim texto As String = ""
For Each item As Object In p
texto &= item.ToString()
Next item
lstResultados.Items.Add(texto)
Next p
txtPermutacoes.Text = Format$(Factorial(num_valores))
End Sub
' Retorna o fatorial do número
Private Function Factorial(ByVal num As Long) As Long
Dim resultado As Long = 1
For i As Integer = 2 To num
resultado *= i
Next i
Return resultado
End Function
' Gera as permutacoes de valores na coleção valores
' Retorna o resultado através da coleção
Private Function GeraPermutacoes(ByVal valores As Collection) As Collection
Dim resultados As New Collection
' Verifica se existe um único valor
If valores.Count = 1 Then
' Retorna uma coleção contendo
' a permutação igual a valor único
resultados.Add(New Collection)
resultados.Item(1).Add(valores.Item(1))
Return resultados
End If
' Cria as permutações iniciando com cada primeiro item
resultados = New Collection
Dim num_valores As Integer = valores.Count
For i As Integer = 1 To num_valores
' Salva o valor
Dim primeiro_valor As Object = valores.Item(i)
' Remove o item.
valores.Remove(i)
' Gera as permuatações dos valores restantes
Dim nova_permutacoes As Collection = GeraPermutacoes(valores)
' Faz a permutação incluino o primeiro_valor
' no inicio de cada nova permutação
For j As Integer = 1 To nova_permutacoes.Count
' Inclui o primeiro item
Dim novo_resultado As New Collection
novo_resultado.Add(primeiro_valor)
' Inclui o resto dos itens na nova permutação
For k As Integer = 1 To nova_permutacoes(j).Count
novo_resultado.Add(nova_permutacoes(j).Item(k))
Next k
' Inclui esta nova permutação aos resultados
resultados.Add(novo_resultado)
Next j
' Restaura o valor removido
If i > valores.Count Then
valores.Add(primeiro_valor)
Else
valores.Add(primeiro_valor, , i)
End If
Next i
' Retorna o resultado
Return resultados
End Function
End Class
|
O código acima possui duas funções que são chamadas a partir do evento Click do botão Calcular Permutações :
Código é trivial e esta comentado mas alerto para fato de que ele não esta otimizado, e para um número maior de itens (maior que 9) o sistema poderá ficar lento e até travar.
Fica como exercício a otimização dos código se realmente isso for de seu interesse.
Pegue os projetos completos aqui : Permutacaoes.zip e Permutacoes2.zip
Eu sei é apenas VB .NET mas eu gosto...
"Graças e Paz da parte de Deus Pai e da de nosso Senhor Jesus Cristo. O qual se deu a si mesmo por nossos pecados para nos livrar do presente século mau, segundo a vontade de Deus nosso Pai, ao qual glória para todo o sempre, Amém." Gálatas 3-5
Referências: